Tumbukan lenting sempurna tuh maksudnya bagaimana sih ? Dua benda
dikatakan melakukan Tumbukan lenting sempurna jika Momentum dan Energi
Kinetik kedua benda sebelum tumbukan = momentum dan energi kinetik
setelah tumbukan. Dengan kata lain, pada tumbukan lenting sempurna
berlaku Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik.
Hukum Kekekalan Momentum dan Hukum Kekekalan Energi Kinetik berlaku
pada peristiwa tumbukan lenting sempurna karena total massa dan
kecepatan kedua benda sama, baik sebelum maupun setelah tumbukan. Hukum
Kekekalan Energi Kinetik berlaku pada Tumbukan lenting sempurna karena
selama tumbukan tidak ada energi yang hilang. Untuk memahami konsep ini,
coba jawab pertanyaan berikut ini.
Ketika dua bola
billiard atau dua kelereng bertumbukan, apakah anda mendengar bunyi yang
diakibatkan oleh tumbukan itu ? atau ketika mobil atau sepeda motor
bertabrakan, apakah ada bunyi yang dihasilkan ? pasti ada bunyi dan
juga panas yang muncul akibat benturan antara dua benda. Bunyi dan
panas ini termasuk energi. Jadi ketika dua benda bertumbukan dan
menghasilkan bunyi dan panas, maka ada energi yang hilang selama proses
tumbukan tersebut. Sebagian Energi Kinetik berubah menjadi energi panas
dan energi bunyi. Dengan kata lain, total energi kinetik sebelum
tumbukan tidak sama dengan total energi kinetik setelah tumbukan.
Nah, benda-benda yang mengalami Tumbukan Lenting Sempurna tidak
menghasilkan bunyi, panas atau bentuk energi lain ketika terjadi
tumbukan. Tidak ada Energi Kinetik yang hilang selama proses tumbukan.
Dengan demikian, kita bisa mengatakan bahwa pada peritiwa Tumbukan
Lenting Sempurna berlaku Hukum Kekekalan Energi Kinetik.
Apakah tumbukan lenting sempurna dapat kita temui dalam kehidupan sehari-hari ? Tidak….
Tumbukan lenting sempurna merupakan sesuatu yang sulit kita temukan
dalam kehidupan sehari-hari. Paling tidak ada ada sedikit energi panas
dan bunyi yang dihasilkan ketika terjadi tumbukan. Salah satu contoh
tumbukan yang mendekati lenting sempurna adalah tumbukan antara dua bola
elastis, seperti bola billiard. Untuk kasus tumbukan bola billiard,
memang energi kinetik tidak kekal tapi energi total selalu kekal.
Lalu apa contoh Tumbukan lenting sempurna ?
contoh jenis tumbukan ini tidak bisa kita lihat dengan mata telanjang
karena terjadi pada tingkat atom, yakni tumbukan antara atom-atom dan
molekul-molekul. Istirahat dulu ah…
Sekarang mari kita tinjau persamaan Hukum Kekekalan Momentum dan
Hukum Kekekalan Energi Kinetik pada perisitiwa Tumbukan Lenting
Sempurna. Untuk memudahkan pemahaman dirimu, perhatikan gambar di bawah.
Dua benda, benda 1 dan benda 2 bergerak saling mendekat. Benda 1 bergerak dengan kecepatan v1 dan benda 2 bergerak dengan kecepatan v2.
Kedua benda itu bertumbukan dan terpantul dalam arah yang berlawanan.
Perhatikan bahwa kecepatan merupakan besaran vektor sehingga dipengaruhi
juga oleh arah. Sesuai dengan kesepakatan, arah ke kanan bertanda
positif dan arah ke kiri bertanda negatif. Karena memiliki massa dan
kecepatan, maka kedua benda memiliki momentum (p = mv) dan energi kinetik (EK = ½ mv2). Total Momentum dan Energi Kinetik kedua benda sama, baik sebelum tumbukan maupun setelah tumbukan.
Secara matematis, Hukum Kekekalan Momentum dirumuskan sebagai berikut :
Keterangan :
m1 = massa benda 1, m2 = massa benda 2
v1 = kecepatan benda sebelum tumbukan dan v2 = kecepatan benda 2 Sebelum tumbukan
v’1 = kecepatan benda Setelah tumbukan, v’2 = kecepatan benda 2 setelah tumbukan
Jika dinyatakan dalam momentum,
m1v1 = momentum benda 1 sebelum tumbukan, m1v’1 = momentum benda 1 setelah tumbukan
m2v2 = momentum benda 2 sebelum tumbukan, m2v’2 = momentum benda 2 setelah tumbukan
Pada Tumbukan Lenting Sempurna berlaku juga Hukum Kekekalan Energi Kinetik. Secara matematis dirumuskan sebagai berikut :
Kita telah menurunkan 2 persamaan untuk Tumbukan Lenting Sempurna,
yakni persamaan Hukum Kekekalan Momentum dan Persamaan Hukum Kekekalan
Energi Kinetik. Ada suatu hal yang menarik, bahwa apabila hanya
diketahui massa dan kecepatan awal, maka kecepatan setelah tumbukan bisa
kita tentukan menggunakan suatu persamaan lain. Persamaan ini
diturunkan dari dua persamaan di atas. Persamaan apakah itu ? nah, mari kita turunkan persamaan tersebut… dipahami perlahan-lahan ya
Sekarang kita tulis kembali persamaan Hukum Kekekalan Momentum :
Kita tulis kembali persamaan Hukum Kekekalan Energi Kinetik :
Kita tulis kembali persamaan ini menjadi :
Ini merupakan salah satu persamaan penting dalam Tumbukan Lenting
sempurna, selain persamaan Kekekalan Momentum dan persamaan Kekekalan
Energi Kinetik. Persamaan 3 menyatakan bahwa pada Tumbukan
Lenting Sempurna, laju kedua benda sebelum dan setelah tumbukan sama
besar tetapi berlawanan arah, berapapun massa benda tersebut.











 bergerak dengan kecepatan masing-masing adalah
bergerak dengan kecepatan masing-masing adalah  , maka kecepatan pusat massa sistem tersebut adalah :
, maka kecepatan pusat massa sistem tersebut adalah :
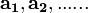 , maka percepatan pusat massa sistem tersebut adalah :
, maka percepatan pusat massa sistem tersebut adalah :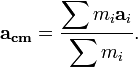
 , maka benda-benda tersebut masing-masing memiliki percepatan :
, maka benda-benda tersebut masing-masing memiliki percepatan :

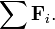 merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem
tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol (
merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem
tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol ( ), maka sistem tersebut tidak dipercepat (
), maka sistem tersebut tidak dipercepat ( ). Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat massa sistem tersebut konstan (
). Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat massa sistem tersebut konstan ( ). Jadi dapat disimpulkan bahwa :
). Jadi dapat disimpulkan bahwa :
